Fórmula general de la ecuación cuadrática
Fórmula general de la ecuación cuadrática
Resolviendo ecuaciones cuadráticas usando la formula cuadrática
La fórmula cuadrática funcionará con cualquier ecuación cuadrática, pero sólo si la ecuación está en la forma estándar, ![]() . Para usarla, sigue estos pasos.
. Para usarla, sigue estos pasos.
· Pon primero la ecuación en su forma estándar.
· Identifica los coeficientes, a, b y c. Ten cuidado de incluir los signos negativos si los términos bx o c se restan.
· Sustituye los valores por los coeficientes en la fórmula cuadrática.
· Simplifica lo más posible.
· Usa el ± en frente del radical para separar la solución en dos valore: uno en el que la raíz cuadrada se suma y el otro en el que la raíz cuadrada se resta.
· Simplifica ambos valores para obtener las posibles soluciones.
Son bastantes pasos. Intentemos usar la fórmula cuadrática para primero resolver una ecuación relativamente simple; luego volveremos a resolver usando otro método de factorización.
Ejemplo | |||
Problema | Usar la fórmula cuadrática para resolver la ecuación x2 + 4x = 5. | ||
| x2 + 4x = 5 x2 + 4x – 5 = 0 |
| Primero escribe la ecuación en su forma estándar. |
|
|
| a = 1, b = 4, c = −5
Observa que el signo de resta significa que la constante c es negativa. |
|
|
| Sustituye los valores en la fórmula cuadrática. |
|
|
| Simplifica, teniendo cuidado de usar los signos correctos. |
|
|
| Simplifica un poco más. |
|
|
| Simplifica el radical: |
|
o
|
| Separa y simplifica para encontrar las soluciones de la ecuación cuadrática. Observa que en una, se suma 6 y en la otra se resta 6.. |
Respuesta | x = 1 o −5 |
|
|
Puedes comprobar estas soluciones sustituyendo 1 y −5 en la ecuación original.
x = 1 | x = −5 |
x2 + 4x = 5 | x2 + 4x = 5 |
(1)2 + 4(1) = 5 | (−5)2 + 4(−5) = 5 |
1 + 4 = 5 | 25 ‒ 20 = 5 |
5 = 5 | 5 = 5 |
Obtienes enunciados válidos, por lo que sabes que ambas soluciones funcionan: x = 1 o −5. ¡Has resuelto con éxito una ecuación usando la fórmula cuadrática!
Sin embargo, al ver x2 + 4x = 5, pudiste haber pensado “ya sé cómo resolver esto; puedo reescribir la ecuación como x2 + 4x – 5 = 0 y luego factorizar como (x + 5)(x – 1) = 0, entonces x = −5 o 1.” Esto es correcto, ¡y felicidades si encontraste esta conexión!
Algunas veces, podría ser más fácil resolver una ecuación usando los métodos convencionales de factorización, como encontrar números pares que se suman a un número (en este ejemplo, 4) y que producen una cantidad específica (en este ejemplo, −5) cuando se multiplican. El poder de la fórmula cuadrática es que puede usarse para resolver cualquier ecuación cuadrática, incluso aquellas donde no se puede encontrar el número de combinaciones.
La mayoría de las ecuaciones cuadráticas que hemos visto han tenido dos soluciones, como la anterior. El siguiente ejemplo es un poco distinto.
Ejemplo | |||
Problema | Usa la fórmula cuadrática para resolver la ecuación x2 – 2x = 6x – 16. | ||
| x2 – 2x = 6x – 16 x2 – 2x – 6x + 16 = 0 x2 – 8x + 16 = 0 |
| Resta 6x de cada lado y suma 16 a ambos lados para poner la ecuación en su forma estándar. |
|
|
| Identifica los coeficientes a, b y c. x2 = 1x2, entonces a = 1. Como 8x se resta, b es negativo.
a = 1, b = −8, c = 16 |
|
|
|
Sustituye los valores en la fórmula cuadrática. |
|
|
| Simplifica. |
|
|
| Como la raíz cuadrada de 0 es 0 y sumar o restar 0 da el mismo resultado, sólo hay un valor posible. |
Respuesta | x = 4 |
|
|
De nuevo, comprueba usando la ecuación original.
x2 – 2x = 6x – 16 |
(4)2 – 2(4) = 6(4) – 16 |
16 – 8 = 24 – 16 |
8 = 8 |

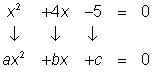
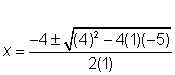
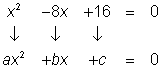
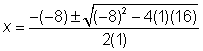



Comentarios
Publicar un comentario